¡Puaj! 26+ Listas de Standard Deviation Formula For Ungrouped Data! The formula for variance and standard deviation for grouped data is very similar to the one for ungrouped data.
Standard Deviation Formula For Ungrouped Data | In this procedure, as a first step it is essential to calculate the mean or average of the data. Calculate the standard deviation of the following data. Variance is defined as the average squared difference from the mean for all data points. 5 6 8 7 4 6 though the range =6. We then use the calculator formula to find the variance the data are plotted in figure 2.2, which shows that the outlier does not appear so extreme in the logged data.
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. Deviation just means how far from the normal. The standard deviation is a statistic that measures the dispersion of a dataset relative to its mean. Standard deviation is similar to the mean deviation, but you cannot treat them as equals. The standard deviation is represented by the symbol σ and can be calculated using the following formula :
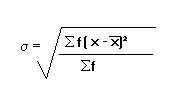
The standard deviation tells you how spread out from the center of the distribution your data is on average. In case of a frequency distribution with as class marks and as the corresponding class frequencies, the from the above methods of calculating standard deviation, both grouped and ungrouped, we have noticed that computing standard deviation requires number. We can also calculate a standard deviation for discrete quantitative variables. Standard deviation is the tendency of the data to differ from the mean. Calculate the standard deviation of the following data. Find standrad deviation for ungrouped data. Formula for mean & standard deviation found in formula sheet. In the second step, the user has to subtract the mean from each observation. In the next two sections, we will apply the formulas on ungrouped and grouped data. The standard deviation plays a dominant role in the study of variations in data. This is the formula for standard deviation: Hope you like above article about formula for variance and standard deviation for ungrouped data and how to calculate variance. We walk you through how to find a sample or population standard deviation.
For example, when conducting a survey where you want to analyze how many women above 50 use social media in a particular area, you first need to. How to find standard deviation by hand? Variance is defined as the average squared difference from the mean for all data points. Variance and standard deviation of ungrouped data example 3. Standard deviation formulas for populations and samples.

Relative standard deviation is a common formula used in statistics and probability theory to determine a standardized measure of the ratio of the standard deviation to the mean. Calculate sample variance `(s^2)`, sample standard deviation `(s)`, sample coefficient of variation from the following data 3,13,11,15,5,4,2,3,2. Variance and standard deviation (ungrouped data). Mean the average of data ungrouped total sum÷n. For example, when conducting a survey where you want to analyze how many women above 50 use social media in a particular area, you first need to. Math·statistics and probability·summarizing quantitative data·variance and standard deviation of a population. The standard deviation is expressed in the same unit of measurement as the data. So, standard deviation of the given data is 6.32. · if the data values are not given directly but the squares of the deviations from the mean of each observation is given then to find standard deviation we can use the formula σ =. The standard deviation is a statistic that measures the dispersion of a dataset relative to its mean. How to find standard deviation by hand? In applying this method first of all we compute the arithmetic mean of the given data, either ungrouped or grouped. This is the formula for standard deviation:
This is the currently selected item. The standard deviation is expressed in the same unit of measurement as the data. Standard deviation for grouped data. This is because the standard deviation measures the spread of the data. Math·statistics and probability·summarizing quantitative data·variance and standard deviation of a population.

It is useful in comparing sets of data which may have the same mean but a different range. Following are the number of students enrolled in english coaching program each month for the last 7 months 24, 21, 29, 18, 26, 20, and 23. The formula for standard deviation becomes: The standard deviation uses the deviation values as once you have the mean, calculate the deviation of each data point by subtracting the mean from each point. Calculate the standard deviation of the following data. In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. The standard deviation measures the spread of the data about the mean value. The formula for variance and standard deviation for grouped data is very similar to the one for ungrouped data. Ungrouped data, on the other hand, is raw data that has not been categorized into groups. It is expressed in the same units as the mean of as students, you might find it confusing to understand the procedures to calculate the standard deviations for grouped and ungrouped data. In applying this method first of all we compute the arithmetic mean of the given data, either ungrouped or grouped. Ungrouped data is the type of distribution in which the data is individually given in a raw form. This formula is useful in various situations including when comparing your own data to other related data and in financial.
This is because the standard deviation measures the spread of the data standard deviation formula. It stands like a tower among measures of dispersion.
Standard Deviation Formula For Ungrouped Data! Relative standard deviation is a common formula used in statistics and probability theory to determine a standardized measure of the ratio of the standard deviation to the mean.
0 Response to "¡Puaj! 26+ Listas de Standard Deviation Formula For Ungrouped Data! The formula for variance and standard deviation for grouped data is very similar to the one for ungrouped data."
Posting Komentar